Yellow on your screen does not exist! Part 1: Chasing rainbows

Physical and mathematical concepts behind the magic of rainbows

One thing about kids is universal – they love to play with rainbows and colored light. It is magical to see how ordinary light turns into colors, or how a laser beam “cuts” through air and glass. We can tap into this interest and attention by showing them physical and mathematical concepts behind the magic.

Multi Color Witchcraft

Welcome to the School of Magic where instead of wands and magic accessories we use lasers, prisms, and small digital USB microscopes. These items can be easily purchased online and used in various STEM activities. I would recommend having them in your “home laboratory”.  

For the safety scale and instructions on writing STEM notes see our previous story. The main safety concern in the experiments described here are lasers. Teach kids to never ever point lasers into eyes and they must be aware where reflected laser beams end up. While older kids can easily adopt this safety habit, smaller kids tend to be more playful and careless.

Our goal is to give kids an introduction into the magic of rainbow colors and then end with the explanation of the color illusion used by digital screens in our TVs, computers, and smartphones. Our story today takes us from simple to more complex concepts that kids can understand and find interesting.

The first concept we need to cover in this “school of magic” is how a ray of light behaves when it travels from one medium into another. This is the same as “bending” of light when you watch a spoon in a glass of water. We just want to be more methodical and see how exactly this bending happens.

You can construct a simple experiment to explore how the bending behaves:

• Take a glassware, or a glass bowl, or a glass jar, preferably with flat sides, and fill it with water.

• Add a drop of milk or pour a little bit of coke into the water. This will help you see the laser beam.

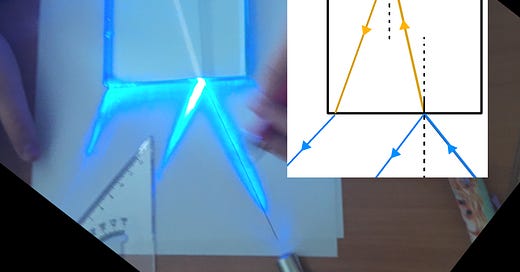
• Shine a laser beam onto the glass and observe how the ray changes its direction. Blue and green lasers are much better for this than red as they are more easily visible in the liquid or within the glass itself.

• Let the kids figure out on their own how the light behaves. Tell them to make sketches and measure angles. Encourage them to pay attention to the details that influence the experiment.

A very nice version of this can be done if you have a block of pure glass. Glass fluoresces under blue (or green) light, and this will make the laser ray clearly visible within the glass (see our previous story on fluorescence).

An experiment with a block of glass and blue laser, demonstrating light reflection and refraction. The glass fluoresces under the blue light (see our previous story), which makes the laser beam clearly visible within the glass. At each contact surface between the two media (air – glass), a fraction of the light reflects (reflection), and the rest passes through the barrier. The light speed slows down in a denser medium (glass), which makes the ray change its direction (refraction). When it exists the denser medium, the speed increases and the ray direction changes again. The sketch shows what happens to the laser in the photo.

Two processes are visible when a laser beam encounters a boundary between two media of different density. One process is light reflection, like in a mirror, where the ray gets reflected with the same exit angle relative to the surface normal as the incoming angle. The second process is refraction, where a fraction of the ray passes through the barrier but changes the path direction because the speed of light is different. Two densities can happen even within the same type of material. For example, hot air over a road exhibits different densities, which bends the light due to refraction. This creates a mirage image.

The change of direction of a ray of light (refraction) when coming from the air and entering a medium (shown in gray). This can be mathematically described with two triangles shown in the image. If we pick the same length L in both triangles, the sides A and B will follow the formula A=n*B, where the number n is called “index of refraction”. Slight differences in this index make different colors of light follow different paths (known as “dispersion”). Here we assumed that the air’s index of refraction is equal to 1, the same as in vacuum.

The magic of colors is hidden in the way how different colors react to this refraction. The light is a wave of electric and magnetic fields, and it interacts with atoms and molecules when traveling through some medium. This interaction slows down the light, which makes the light change its direction when entering the medium.

If this slower speed is v, and the maximum speed is c, happening in vacuum, then we can introduce the index of refraction n=c/v. This index tells us how much a ray of light will bend according to the formula known as the Snell’s law. A simplified version of this formula, useful for our home laboratory experiments, is shown in the figure above. The air has n=1.0003, so for our practical purposes here we can say it is equal to 1. Water has approximately n=4/3, while the glass is approximately n=3/2.

The inability of light rays to bend into arbitrary directions results in a phenomenon of total reflection, where a ray cannot exit a higher density medium. This is how a waveguide works and guides light through an optical fiber.

A homemade waveguide. If you shine a laser light into a water container from a side (A), the light can get trapped because of total reflection. There are no angles into which the light could exit the water (B) and it can only bounce back. When it encounters the water-glass barrier, where the index of refraction difference is small (E), the ray can enter the glass. But then it again has a problem with exiting into the air (D), so it bounces within the glass. After that it crosses the glass-water barrier (C) and enters the water.

Each hue of rainbow colors can be described by the wavelength of light, which measures the distance between two adjacent crests of the electric or magnetic field wave traveling in a vacuum. For visible light it spans from about 380 nanometers (nm; one-billionth of a meter) to about 740 nm. We call this “spectrum”, and it is a continuous range of colors, with no clear boundaries between them. Hence, the attachment of light wavelengths to specific colors is not exact and it depends on our individual sense of color and cultural differences in naming colors. Approximately, we can say that (notice the conflict between violet and indigo, or cyan and green): violet=380–450 nm, indigo=435-450 nm, blue=450–495 nm, cyan=490–520 nm, green=495–570 nm, yellow=565–590 nm, orange=590–625 nm, red=625–740 nm.

Rainbow chasers

The fun part here is that different colors have a slightly different index of refraction. This means that a light ray composed of a mixture of colors will break into a bundle of rays, where each color follows its own path. So, why don’t we see rainbow colors everywhere? It turns out that it is not so easy to avoid mixing of those colors back into the original mixture. When they exit the medium (water, glass), they bend back into the original direction and get mixed. Also, we do not send one ray of light – our light sources, like a bulb or a flashlight, send light rays in many directions, which prevents us to see a narrow beam of nicely separated colors.

An experiment with a rainbow visible in a glass tank filled with water. The flashlight (A) has a cover made of aluminum foil with a narrow slit. We observe the light from the other side of the tank. The bottom photo shows the view of unobscured source A and its position B visible through water because of the light bending. At the same time, when we look toward the direction C, a rainbow is visible. This happens because rays of different colors are unable to mix themselves back into white light when exiting the tank along the path C.  

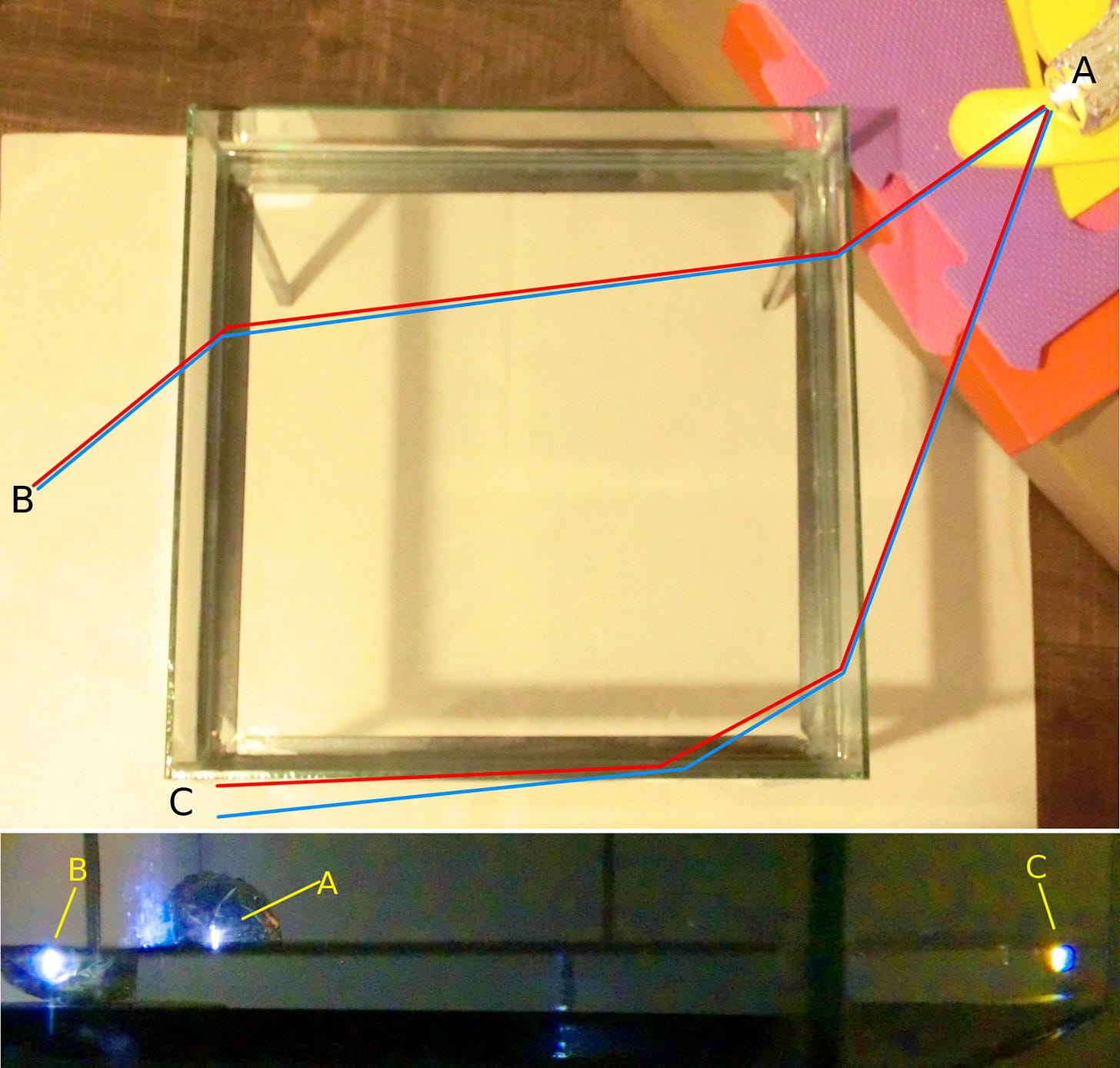
To make rainbows visible, we must make small adjustments in our experimental setup:

• Take a flashlight and make a simple cover with a slit to create a narrow beam of light. You can simply get an empty toilet paper roll and cover it on one side with aluminum foil that has a narrow slit (made with a sharp knife).

• Take a water tank, or a glass bowl, or a jar, fill it with water.

• Shine the narrow beam of light onto it and start looking for a rainbow somewhere at the edges of your water tank.

You can be sure that a rainbow is lurking somewhere around this setup. Take a white sheet of paper and try to find it.

Rainbow from a jar of water. The flashlight (A) has a cover made of aluminum foil with a narrow slit. The jar (B) simulates a raindrop that produces a rainbow (C). The photo on the right shows the same experiment, but with a blue laser. The small image illustrates the laser light path with arrows.

A very successful “device” for producing rainbows is a simple glass prism. It is a very handy tool for decomposing light into constituent colors. This color “content” of a light source is called spectrum, and it can reveal lots of information about the physical nature of the source. For example, astronomers can decipher a star’s size, temperature, and chemical composition just by studying its spectrum.

A blue laser shining on a prism. The laser beam (1) hits the prism surface and gets partially reflected (2) and refracted (3). The refracted ray then encounters the other side of the prism and again gets partially reflected (5) or refracted (4). The newly reflected ray goes through the same process (7,6), producing another internally reflected ray. In this sketch the ray exits the prism (8) after two internal reflections (5,7).

Showing the spectrum of a mobile phone light to the kids in a kindergarten.

Now we are ready to tell the story of real rainbows in the sky. The story is a version of the experiment with a jar of water that behaves like a prism. Except that now we have millions of water droplets in the sky, with each of them refracting the sun’s light. With just the right position of the sun behind us as we observe from the ground, and raindrops in front of us, we can see the colors coming out of spherical droplets. By the way, raindrops have a spherical shape, with bigger drops becoming flattened by air drag. 

If you draw paths of parallel rays entering a spherical water droplet, you will notice how many rays reflected within the sphere concentrate around the “magical” outgoing angle. This angle differs slightly for different colors, which results in a color dispersion visible as rainbow.

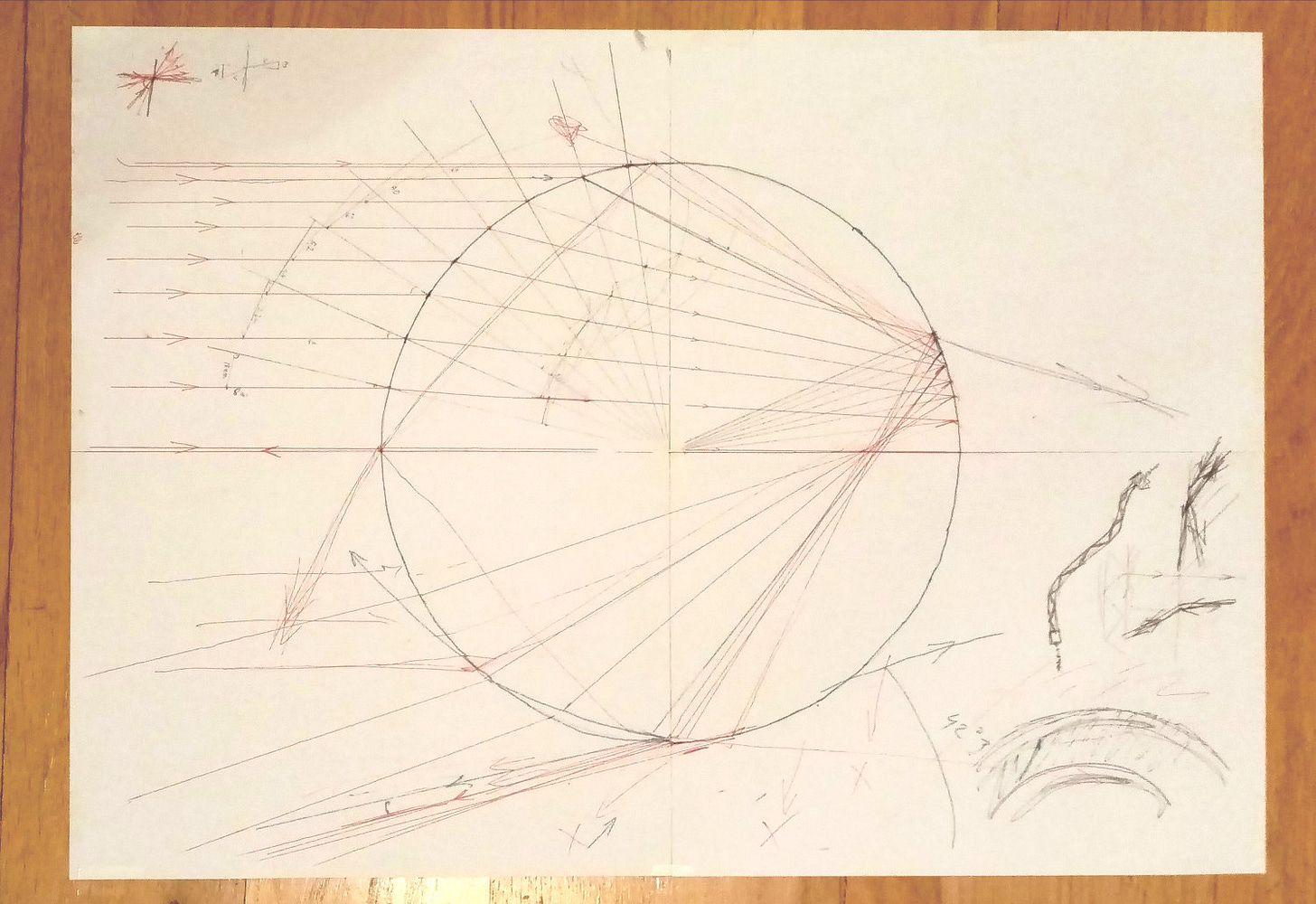
An important detail in rainbows is that a circular object (a spherical droplet or a cylindrical jar) bend (i.e., refract) incoming parallel light rays in such a way that many of them concentrate close to a “magic” outgoing angle. This angle varies between 40° for violet and 42° for red as different colors travel along slightly different paths. All the colors of rainbow squeeze between these two angles, and, therefore, rainbows always appear to have the same angular size in the sky. For the same reason, the sun must be below 42° above the horizon for a rainbow to appear. Or you can use a garden hose and sprinkle water in front of you. A rainbow will appear if the sun is behind you.

It was René Déscartes in 1637 who realized that rainbows are a result of this magical angle. He also calculated the second magical angle (between 50° and 53°), produced by double reflection of light within a sphere of water, which makes the secondary rainbow. However, he didn’t know about color dispersion. People thought that glass or water colored light, which was supposed to be a mixture of light and darkness. In 1670’s Isaac Newton published results of his experiments with prism and sunlight, where he explained that light consists of different colors. Interestingly, already during these first discussions about the nature of light refraction, the issue of finite light speed was raised. Déscartes assumed the infinite speed of light, which was problematic when he derived the bending of light in a dense medium. At the same time, the famous Pierre de Fermat argued the opposite – that the light speed is limited, and it gets slower in a denser medium.

Primary and secondary rainbow. The sun shines on a curtain of rain in front of us, where a fraction of sunlight is bended within the raindrops and sent back to us. If the rays reflect only once within raindrops, we see the primary (brighter) rainbow. Differences in the index of refraction result in the colors seen along different angles (40°-42°) relative to the direction of sunlight. If the rays reflect twice within raindrops, we see the secondary (dimmer) rainbow (within 50°-53°).

Notice the difference between the primary and secondary rainbow. The primary is created when the rays are reflected only once within raindrops, and we call this the first order bow. A smaller fraction of light is internally reflected twice, and this is the secondary or the second order bow. In case of no reflection, the light passes through the rain and produces the zero order glow (visible towards the sun). It has been thought for a long time that this is all we can see when it comes to rainbows because the third and fourth internal reflections lose too much intensity to be seen. Even worse, they should be visible toward the sun. The 5th and 6th order should appear again close to the primary and secondary rainbow, but with extremely low intensities.

But then, in 2011, the first proofs of detected third order (tertiary) and fourth order (quaternary) rainbows were published! It required skill, luck, and digital image enhancements to demonstrate their existence. Amazingly, soon after that the first proof of the fifth order (quinary) rainbow was published. There is now a whole new race to image the higher order rainbows, which requires more sophisticated equipment and techniques. Interestingly, in a laboratory we can observe many more higher order rainbows using lasers as the light source – up to the 200th order has been measured.

In Part 2 of this story we will explain how our brain tricks us when we see colors.

And then, we will talk about the shocking truth about rainbows - the story I told you cannot explain all the colors that can appear in a rainbow! For that we need a more advanced theory of light.